Formula for Area using Definite Integrals
The Area A of the region bounded by the curves y = f(x), y = g(x) and the lines x = a, x = b, where f and g are continuous f(x) >=g(x) for all x in [a, b] is
Example:
Find the area of the region bounded above by y = x2 + 1, bounded below by y = x, and bounded on the sides by x = 0 andx = 1.
Solution:
The upper boundary curve is y = x2 + 1 and the lower boundary curve is y = x.
Using the formula,
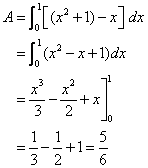
Area between Curves
Example:
Step 1: Find the points of intersection of the two parabolas by solving the equations simultaneously.
x2 = 2x – x22x2 – 2x = 0
2x(x – 1) = 0
x = 0 or 1
2x(x – 1) = 0
x = 0 or 1
The points of intersection are (0, 0) and (1, 1)
Step 2: Find the area between x = 0 and x = 1
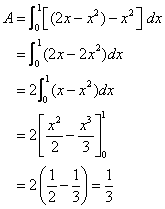
Calculus - Finding the Area Under the Curve
Example 1
Example 2
Find the area under the curve y = x2 - 2x + 8 from x = 1 to x = 2
Find the area under the curve y = x2 - 2x + 8 from x = 1 to x = 2
Calculus - Finding the Area Under the Curve
3 and then from x = -2 to 2
Calculus - Finding the Area Under the Curve
x = π
Calculus - Finding the Area Under the Curve
Find the area under the curve y = sin x cos x from
x = π/4 to x = π/2
Find the area under the curve y = sin x cos x from
x = π/4 to x = π/2
Calculus - Finding the Area Under the Curve
Find the area under the curve y = x2/&rad;(x3 + 9)
from x = -1 to x = 1
Find the area under the curve y = x2/&rad;(x3 + 9)
from x = -1 to x = 1
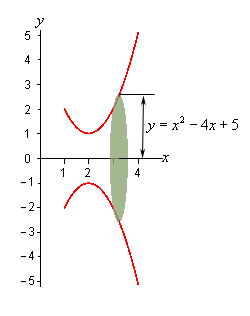
Area bounded by a curve and a line
Find the area bounded by the curves y = x2 - 6x + 9
and y = x + 3.
and y = x + 3.
Solution:
 Example 2 Determine the volume of the solid obtained by rotating the region bounded by
Example 2 Determine the volume of the solid obtained by rotating the region bounded by
Solution
The first thing to do is get a sketch of the bounding region and the solid obtained by rotating the region about the x-axis. Here are both of these sketches.
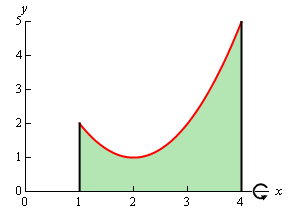
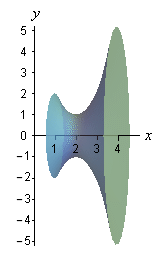
Okay, to get a cross section we cut the solid at any x. Below are a couple of sketches showing a typical cross section. The sketch on the right shows a cut away of the object with a typical cross section without the caps. The sketch on the left shows just the curve we’re rotating as well as its mirror image along the bottom of the solid.
In this case the radius is simply the distance from the x-axis to the curve and this is nothing more than the function value at that particular x as shown above. The cross-sectional area is then,
Next we need to determine the limits of integration. Working from left to right the first cross section will occur at x = 1 




The volume of the soild is then,
The volume of the soild is then,



Example 3 Determine the volume of the solid obtained by
rotating the portion of the region bounded by
Solution
First, let’s get a graph of the bounding region and a graph of the object. Remember that we only want the portion of the bounding region that lies in the first quadrant. There is a portion of the bounding region that is in the third quadrant as well, but we don't want that for this problem.
 
There are a couple of things to note with this problem. First, we are only looking for the volume of the “walls” of this solid, not the complete interior as we did in the last example.
Next, we will get our cross section by cutting the object perpendicular to the axis of rotation. The cross section will be a ring (remember we are only looking at the walls) for this example and it will be horizontal at some y. This means that the inner and outer radius for the ring will be x values and so we will need to rewrite our functions into the form x = f(y)
  Here are a couple of sketches of the boundaries of the walls of this object as well as a typical ring. The sketch on the left includes the back portion of the object to give a little context to the figure on the right.  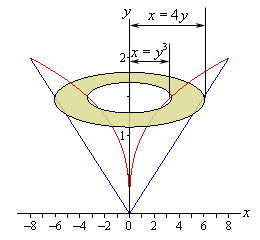
The inner radius in this case is the distance from the y-axis to the inner curve while the outer radius is the distance from the y-axis to the outer curve. Both of these are then x distances and so are given by the equations of the curves as shown above.
The cross-sectional area is then,
Working from the bottom of the solid to the top we can see that the first cross-section will occur at
   |
 Practice questions
Practice questionsDetermine the volume of the solid obtained by rotating the region bounded by the given curves about the given axis.

2. Rotate the region bounded by 











3. Rotate the region bounded by 







2. Rotate the region bounded by 











3. Rotate the region bounded by 














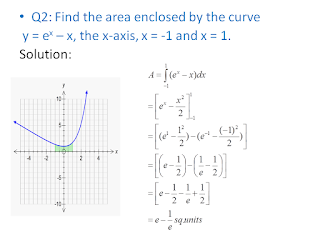
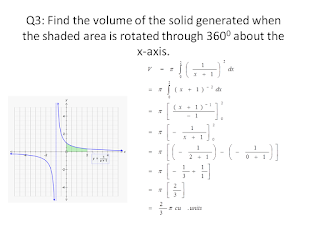










No comments:
Post a Comment