Further integration & trapezium rule
The problems of finding gradients of curves and of finding areas under curves may not at sight, seem connected, but calculus solves both these problems. As we have seen, differentiating gives gradient of curves. In this chapter we will show how integration gives the area under the curve.
This powerful tool enables, for example, the area of an aeroplane's wing to be calculated precisely and is widely used in numerous fields such as economics and engineering.
Evaluate a definite integral
Properties of Definite Integrals
The following properties are helpful when calculating definite integrals.
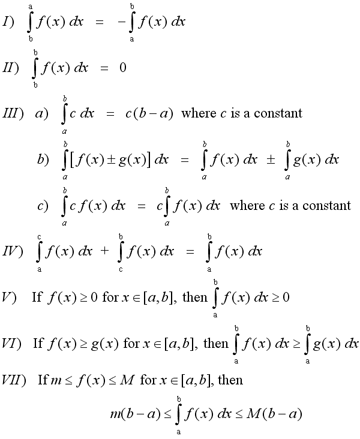
Example of definite integral:
Area Under a Curve by Integration

![Area Between Two CurvesLet f and g be continuous functions such that f(x)>g(x)on the interval [a,b]. Then the area of the ...](http://image.slidesharecdn.com/integration-areaunderacurve-121110020510-phpapp01/95/integration-area-undera-curve-6-638.jpg?cb=1352513146)
![Fundamental Theorem of Calculus• If f is continuous on [a,b], then the definite integral is b a ...](http://image.slidesharecdn.com/integration-areaunderacurve-121110020510-phpapp01/95/integration-area-undera-curve-7-638.jpg?cb=1352513146)
Example:
Trapezium Rule
Formula:

Example :
Use the trapezium rule with 4 intervals to find an approximation to the area bounded by the curve
y = 2^x, the x-axis, x = - 2 and x = 2.
Solution:


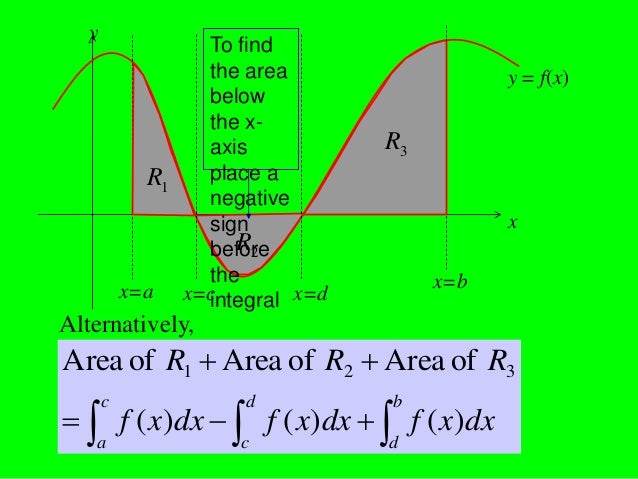
![f(x) < 0 for some interval in [a,b] b a f ( x)dx Area of R1 Area of R2 Area of R3 y ...](http://image.slidesharecdn.com/integration-areaunderacurve-121110020510-phpapp01/95/integration-area-undera-curve-4-638.jpg?cb=1352513146)







No comments:
Post a Comment