Chapter 3- Application of differentiation

Topic: Application of Differentiation.

Increasing function;

For x > 0, y increases as x increases.
The gradient is positive
y is an increasing function of x,  f '(x) > 0
( dy/dx > 0)

Decreasing function:

For x < 0, y decreases as x increases.
The gradient is negative
y is a decreasing function of x, f ' (x) < 0 
( dy/dx < 0)

Q1: Find f '(x) and the range of values of x for which f(x) is increasing.

Q2: Find f '(x) and range of values of x for which f(x) is decreasing.

More questions

Q3: Find f '(x) and the range of values of x for which f(x) is increasing.
f(x)= 2 - 4x - 4x^2

Q4: Find f '(x) and the range of values of x for which f(x) is decreasing.
f(x) = 4 + 3x - 7x^2

  Maximum and Minimum stationary point.

Stationary points:

At a stationary point on the curve the gradient of the curve is zero.

Maximum stationary point:

Q: Find the coordinates of any stationary points on the curve 
y = ( x + 2)^2 and state giving reasons whether each point is a maximum or a minimum.

More Examples:

Q: Find the coordinates of the points on the given curve where gradient is zero.
a) y = x^2 +6x + 7                         b) y=x^4 - 2x^2 +5

Q: Find the range of values of x foe which y = 3x^3 - 9x +2 is decreasing.

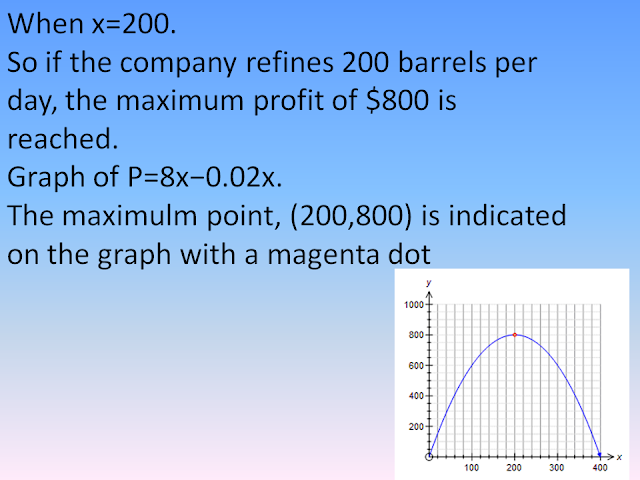
 Solving maximum and minimum problems by using differentiation 

To tackle such problems follow these steps.

• Draw a diagram if relevant.
• Choose letters to represent unknown quantities.
• Express the quantity ( e.g. y) to be maximised or minimised in terms of just one variable (e.g. x).
• Differentiate y with respect to y.
• Solve dy/dx = 0 to find the value(s) of x at maximum or minimum point(s).
• Substitute the value(s) of x in the expression for y,checking that the value(s) give possible answer.
• Check if necessary , that the values gives maximum or minimum.

Q1: An aeroplane  flying level at 250m above the ground suddenly swoops down to drop supplies, and then regains its former altitude. It is h meter above the ground t s after beginning its dive, where

. 
Find a) its least altitude during its operation.
           b) the interval of time during which it was loosing its height.

so, h = 50 m is the least altitude during this operation.

b) Initial time was zero ,t = 0
At minimum height t = 5
There fore, aeroplane looses its height during the time interval 0 < t < 5.

More examples:

You can also look into

Games:

http://www.bbc.co.uk/bitesize/higher/games/wave_rider/